
Innhold
- Zipfs lov forklart
- Grunnleggende eksperiment
- Zipfs lov i dampmarkeder
- Hva kan vi lære om Steam?
- konklusjoner
For en kort tid siden foreslo en venn av meg at jeg så på Vsauces-video på Zipfs lov, Paretos prinsipp og deres mystiske skikkelser rundt oss. Her er en liten teaser for å få oppmerksomheten din - 80% av alle bor i 20% av de mest populære byene; 80% av hele landet tilhører 20% av de rikeste utleiere; 80% av alt søppel er på de 20% tøffeste gatene - som forutsatt av Zipfs lov og Paretos prinsipp.
Ikke nok? Vel, da jeg oppdaget i går, stopper kaninhullet ikke der ... Full av skepsis, bestemte jeg meg for å se på hvor mye tid folk spenderer å spille Steam-spill ... Vel. 80% av folks tid er brukt til å spille 20% av de mest populære spillene ... Interessant? Vel, les videre, det er mer til denne historien.
Klokka på over 20 minutter, er Vsauces forsøk fantastisk og forklarer mange av de store bildene om Zipf, men han er veldig sjenert på å vise oss kjernemekanismen som allment antas å bidra til hvorfor Zipf jobber med hvordan det gjør. Så før vi går videre, vil jeg kort sagt forklare det.
Zipfs lov forklart
Det er flere konseptuelle måter å forklare intuisjonen bak 20/80 prinsippet. Det beste eksemplet, etter min mening, er det om Moon craters.
Grunnleggende eksperiment
Så, tenk hvis du vil, at det er en uberørt Moon - en perfekt jevn overflate. Nå, si at det er noen tilfeldig størrelse asteroider som treffer Månen vilje-nilly. Når den første asteroiden lander, går det et krater. Nå treffer en annen en krater andre steder. Hvert krater er en del av det totale arealet, derfor er det en sjanse for at neste tilfeldige asteroide vil slå nær et eksisterende krater og delta i det, og danne en gruppe. Sjansen for en ny asteroide som treffer et gitt krater er da proporsjonalt med kraters og asteroider av eksisterende størrelse. Dette betyr at neste tilfeldige asteroide er mer sannsynlig å bli med den største eksisterende gruppen, noe som gjør den enda større. En slags kumulativ prosess, som da skaper en rik-rikere-fattig-enklere-mekanisme.
Husk det, fordi det antas å være den generelle forklaringen på "hvorfor" Zipfs lov arbeider med en så mystisk universalitet. Asteroid-eksemplet er ganske enkelt, men spørsmålet er hva som vil skje over mange gjentakelser
Litt forvirrende?
Vel, jeg laget et gif for å kjøre dette utgangspunktet hjemme. NB! grafen vil bli diskutert senere, bare prøv og bilde eksperimentet.

Hvis vi observerer den faktiske Månen, viser det seg at, da mengden asteroider øker til store mengder, observeres kraterdiametrene slik at de øverste 20% av de største kratrene nærmer seg 80% av hele overflaten.
Så når vi går til flere asteroider nærmer distribusjonen av de mest populære til minst populære gruppene en slags "ideell fordeling" med denne 20/80 eiendommen - en Pareto-distribusjon. Hvis du gjør matte, viser det seg at (generelt), hvis den største gruppen har størrelse N, er den nest største gruppen rundt størrelse N / 2, den tredje N / 3 og så videre og så videre. Dette kalles Zipfs lov. Den rare tingen er Zipfs lov og Pareto-distribusjon fungerer for en forvirrende mengde elementer (asteroider) og grupper (kraterklynger). Selvfølgelig er det skjevheter og tilfeldige forstyrrelser, men den generelle trenden er ubestridelig.
Jeg håper du kan se hvordan asteroider som er mer sannsynlig å slå store kratere på månen, forbinder at byene blir mer attraktive, hvis det allerede er flere som bor i dem. Men man må innse at byer er langt fra de eneste "gruppene" som oppfører seg i henhold til Zipf.
Her er noen eksempler fra Mark Newmans forskning på Pareto distribusjoner. NB! Grafer er i logg-skala som jevner ut den hyperbolske formen av kurvene, og presenterer et nesten lineært forhold.
Innledende y = aX ^ (- b)
Logger på begge sider => logg y = logg a - b logg X
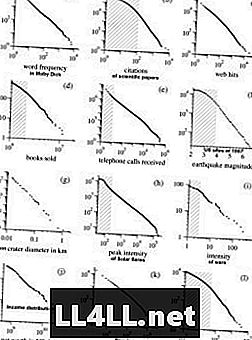
Interessant nok vises også den samme trenden av religiøse kulturer ... Den felles egenskapen til de fleste av disse fenomenene er ganske enkelt denne "store gruppens" større tendens. Så Zipfs lov er vedvarende i mekanismer, hvor preferansene til elementene er positivt knyttet til gruppestørrelsen (dvs. jo større gruppen, jo mer sannsynlig vil den vokse). Derfor liker jeg å tenke på grupper som klynger og elementer som klynger.
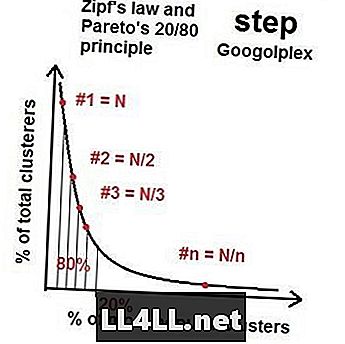
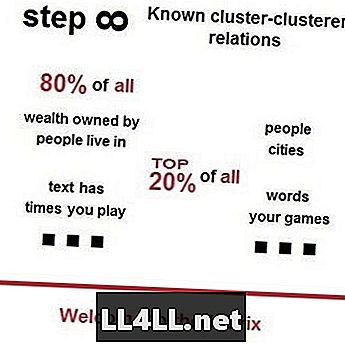
Zipfs lov i dampmarkeder
Mistanke om den siste? Her er hvor mye tid folk bruker på de mest populære spillene på Steam .. Data fra SteamSpy.
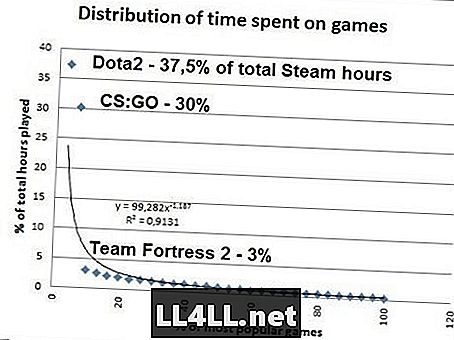
Hvis du gjør matematikken, viser det seg at 20% av de mest populære Steam-spillene står for 80% av den totale mengden av spill, slik at Pareto 20/80-mysteriet fungerer som en sjarm her ... Man må legge merke til, Zipf å være sant, CS: GO må utgjøre 37,5% / 2 = 18,8% av total tid i stedet for 30%. Men bortsett fra denne outlier (STOPP SPILLING CS: GO), den Zipf-lignende distribusjonen er tydelig der.
Her er mengden eksemplarer solgt for de mest populære spillene.
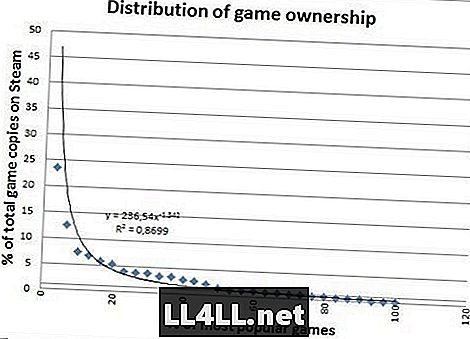
Ser mye finere eh? Eksemplarer som selges, har ikke store utliggere, så det passer veldig bra, noe som er en bemerkelsesverdig forskjell. Det er imidlertid noe mer interessant å konkludere med forskjellene i de to siste grafene.
Legg merke til hvordan "halen" til høyre er litt fett i den andre grafen? Vel, i enkle termer, forteller dette oss at de "relativt upopulære" spillene faktisk er ganske mye mer populære enn i forrige plot.
Faktisk viser det seg at 20% av de mest populære spillene står for bare 60% av salget, mot 80% av spillingen. Interessant? Du satser på det du har, det er.
Hva kan vi lære om Steam?
Vel, det faktum at spillet popularitet følger Pareto distribusjon forteller oss at det faktisk er en slags positiv nettverkseffekt, noe som gjør at spillerne velger spill som allerede spilles av flere mennesker. Hva forskjellen i tetthet av haler forteller oss er at Steam-brukere er mye mer "gruppe-størrelse-blind", når de kjøper spill enn de er når de spiller dem.
Tenk på det - jo flere folk kjøper spill uavhengig av "nåværende populær mening", jo mer flatet ut Pareto-distribusjonen blir, da det er mindre sannsynlig for store spill å vokse videre. Hvis ingen ga en rotte rumpa om hvor mange som allerede spiller et spill og tilgjengeligheten av alle spillene var de samme, ville vi forvente at 20% av de mest populære spillene skulle tegne seg for rundt 50% av salg og spilletid (forutsatt at individuelle preferanser er normalt distribuert).
konklusjoner
Så det er to faktorer som bidrar til Pareto-distribusjonen i Steam-markedene - hvor nyskapende utviklerne er (hvor mange nye månekratere blir dannet) og hvor mye spillerne (asteroider) verdsetter gjeldende gruppestørrelse når de velger hvilken gruppe som skal delta . Som det viser seg, er spillere veldig gruppe-size-blind når de kjøper spill, men bare det motsatte når de spiller dem. Kul huh?
Hvis du vil lære mer om Zipfs lov- og strømloverfordeler, er det et fint foredrag. Videre, sørg for å se på Newmans papir!
Hvis du vil lese mer om denne typen ting, vil jeg snart nok prøve å bli med i denne observasjonen til en modell, som viser at flere populære multiplayer-spill har høyere priser (som kobler til spillernes preferanse for å bli med i større grupper). Se artikkelen her. The Piece De Resistance-artikkelen vil forsøke å bli med i disse teoriene og forklare hvordan multiplayer-spill, sosiale nettverk og byer faktisk er alle anti-konkurrerende varer med nettverkseffekter, (jo mer folk bruker en god, jo mer hver enkelt forbruker fordeler) som har rettet dem med denne Zipfian-tåken av mysterium ...
Inntil da - nyt dere!
PS! Pop i en kommentar med en morsom ide for en 20/80-relasjon du tror kan være sant.
Mine er:
80% av folks nostalgi er forårsaket av 20% av sine lykkeligste minner (faktisk bevist for den prisen folk glemmer informasjon på)
80% av massen er konsentrert i 20% av de største romobjektene (faktisk bevist for fordeling av gravitasjonskraft)
Og selvfølgelig
80% av rotet på toalettet kommer fra 20% av hva du spiser (ingen akademisk forskning for å snakke om)